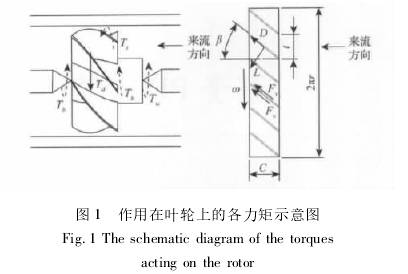
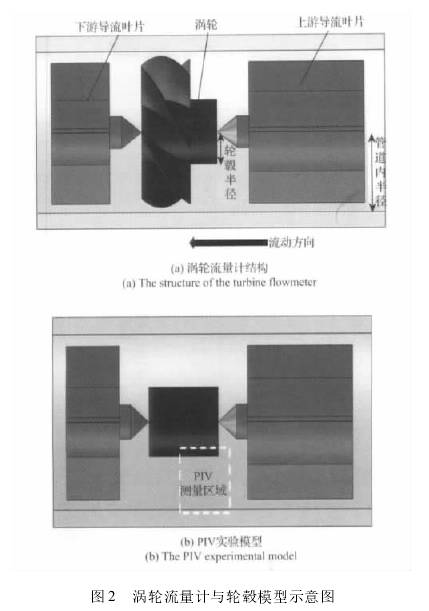
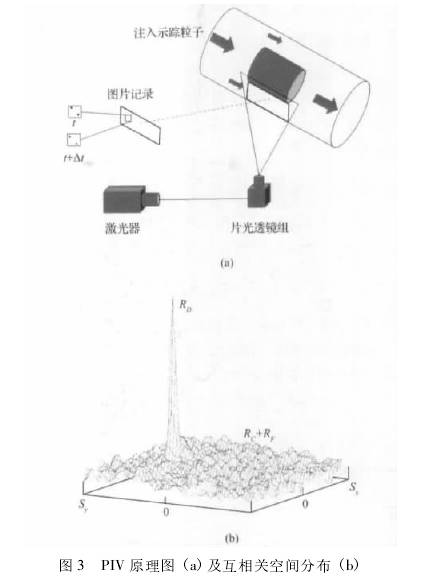
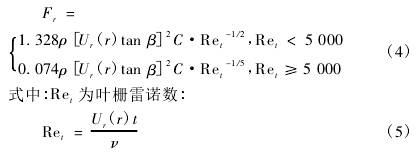|
| 電磁流量計的工作原理 | |
| 氧化鋯氧傳感器的原理及應用 | |
| 有害氣體檢測報警儀選用原則 | |
| 我國計量用儀器儀表的發展和現狀 | |
| 國內儀器儀表行業將發生高科.... | |
| 西安交大研制出超高溫沖擊壓.... | |
| 采用半導體精密溫度傳感...... | |
| 智能溫度傳感器的發展趨勢 | |
| 簡述幾種氣體檢測傳感器..... | |
| 利用傳感器技術制造智能服裝 | |
| 新型傳感器監控魚群數量 | |
聯系方式 |
| 電話(市場部):0517-86851868 |
| 0517-86882048 |
| 0517-86881908 |
| (拓展部):0517-86882683 |
| 傳真:0517-86851869 |
| 節假日商務聯系電話: 何經理:13655238295 劉經理:15861721324 |
| 郵編:211600 |
| 網址:http://0865117.com/ |
| http://www.sukeyb.com/ |
| E-mail:china-suke@163.com |
| sukeyb@163.com |
| 地址:江蘇省金湖縣工業園區環城西 路269號 |
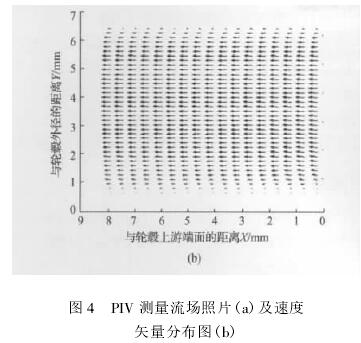
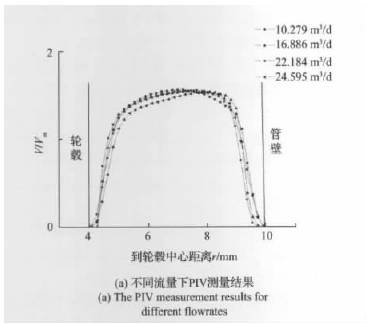
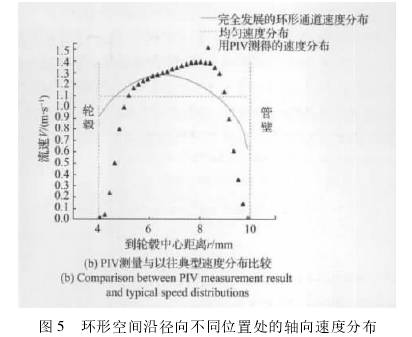
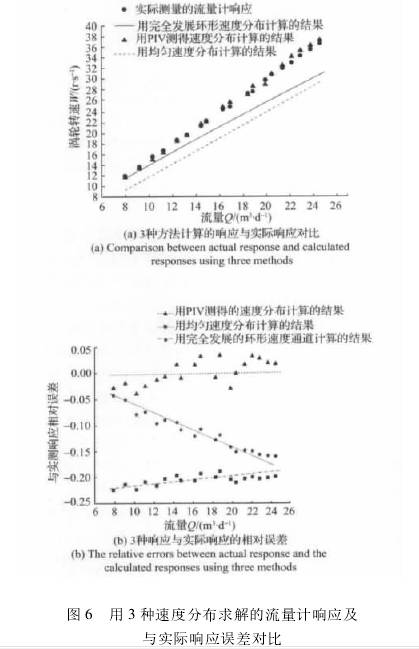
| 您現在的位置 > 首頁 > 行業新聞 > 基于PIV測量的渦輪流量計響應分析 |
|