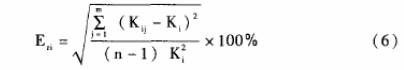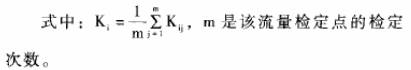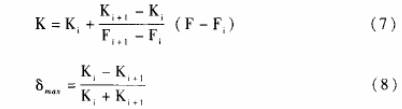摘要:渦輪流量計是應用廣泛的流量計量儀表。它的結構簡單、靈敏度高、壓力損失小。特別是其良好的重復性、穩定性倍受用戶的青睞。但是長期以來，由于其非線性特性的存在，使其流量測量范圍受到很大制約。通過對渦輪流量計輸出脈沖信號特性的研究和分析，提出了一種擴大渦輪流量計量程范圍的方法，這種方法簡單易行、行之有效并可應用于其他脈沖頻率輸出的傳感器中去。
1渦輪流量傳感器的工作原理
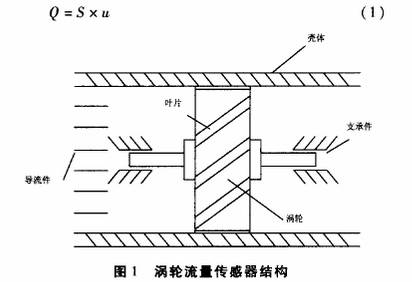
渦輪流量傳感器結構如圖1所示，屬于速度式流量傳感器。渦輪置于流體通道中，隨著流體的流動產生旋轉，設渦輪的轉速為n、流過渦輪的流體速度為u,則n與u成正比;流體通道的流通截面.積S是已知的常數，所以，流過渦輪流量傳感器的流體體積流量Q為:
測量流體速度u通常是利用電磁感應原理將與流體速度成正比的渦輪轉速n變成脈沖頻率F:
F=Nxn(2)
公式(2)中，N是渦輪流量傳感器的葉片數，n是葉輪的旋轉速度。渦輪流量傳感器一旦選定，其葉片數N即為常數，所以信號頻率F與轉速n呈線性關系;由于葉輪的轉速n正比于流體的流速u,對于截面積S恒定的流通管路，由公式(1)可見，流體速度u與流量Q之間也呈線性關系。所以，電脈沖信號頻率F也就正比于流量Q。在使用渦輪流量傳感器時，只要測量出它的輸出電脈沖信號頻率F，就可以計算出相應的體積流量Q。
雖然電脈沖信號頻率F與體積流量Q是正比關系，但是其比值卻不是常數。其原因是流體的摩擦阻力、粘滯阻力、磁電轉換器的電磁阻力以及渦輪軸與軸承之間的機械摩擦阻力等都與流體的流動速度有關。可以用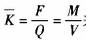
來表達各參數間的關系。
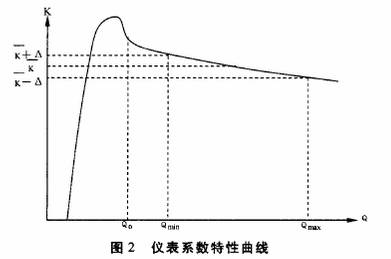
式中，M是渦輪傳感器輸出的電脈沖數，V是流過渦輪傳感器的流體體積，即`K為通過單位流體流量渦輪流量傳感器發出的電脈沖頻率或單位體積流體渦輪流量傳感器發出的電脈沖數，`K稱為渦輪流量傳感器的平均儀表系數。圖2表示了`K與Q之間的關系。以往常規使用方法是在渦輪流量傳感器的測量范圍Qmin一Qmax內，測得各流量檢定點的儀表系數Ki并將各Kt取平均值得到`K，把`K作為該傳感器的平均儀表系數。進行流量測量時，測得渦輪流量傳感器發出的電脈沖頻率F，即可由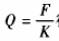
得到相應的流量Q值，從而完成流量測量任務。
2渦輪流量傳感器的測量范圍
圖2顯示測量出電脈沖信號頻率F用平均儀表系數`K計算得到的Q值，在Qmin~Qmax范圍內的最大相對誤差為:
在Q<Qmin或Q>Qmax，即在測量范圍之外誤差將超過δmax。這就是說雖然渦輪流量傳感器具有很好的重復性，但是由于電脈沖信號頻率F與體積流量Q之間是非線性的，按照常規的平均儀表系數`K的計算方法，對于一定的誤差限士A，由于非線性誤差的存在使得渦輪流量傳感器的工作范圍只能限定在Qmin~Qmax之內。
對于重復性很好而線性度較差的渦輪流量傳感器，要擴大其測量范圍或減小測量誤差，研究的核心問題是設計一種便捷的使用方法，按照行鑒定規程利用原有檢定數據，使渦輪流量傳感器在具有很小重復性誤差的流量范圍內，都能得到很準確測量效果。
3渦輪流量傳感器的常規使用方法
像其它速度式流量計一樣，渦輪流量傳感器出廠時要按照渦輪流量傳感器鑒定規程(JJG198-94)的規定進行計量性能檢定。傳感器的量程比a
按照公式(5)計算得到非線性誤差δ≤1.0%,對于量程比a=10的渦輪流量傳感器，很難實現。即采用平均儀表系數`K計算流量的計量精度達到1.0級水平是一件很難是達到的指標;而實際檢定數據顯示，各流量檢定點Qi上的儀表系數Ki的重復性誤差Eri基本都能達到0.1%甚至0.01%范圍之內。Eri由公式(6)計算得到。
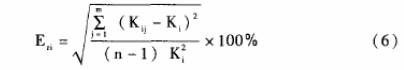
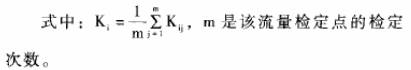
渦輪流量傳感器的重復性誤差Er=Enmax
通常情況下，渦輪流量傳感器的量程比a=10、非線性誤差δ≥1.0%而重復性誤差Er≤0.01。如果在使用渦輪流量傳感器進行流量測量時不對儀表系.數取平均值，即不用平均儀表系數`K而是直接使用各流量檢定點的檢定儀表系數Ki，就有可能避免非線性誤差對流量測量的影響。渦輪流量傳感器的測量誤差就有可能從線性度δ=1.0%變為重復性Eri=0.01%。即渦輪流量傳感器的制造工藝不變、遵循現行的計量檢定規程、使用現有的檢定數據，只是對檢定數據的使用方法稍加改變就有可能成百倍地提高測量精度。
渦輪流量傳感器輸出的脈沖信號頻率F=Nxn(N是渦輪葉片數，n是渦輪的旋轉速度);流過渦輪流量傳感器的被測流體體積流量Q=Sxu(S是流體的流通截面積，u流體介質的流速);渦輪流量
輪流量傳感器的儀表系數K與Q的關系近似線性的單調函數(見圖2)。因此，在對檢定結果進行處理時，直接將各檢定點的檢定結果以Fi、Ki的形式存入渦輪流量計的數值運算部分，不必對其儀表系數取平均值。在使用渦輪流量傳感器進行流量測量時，根據渦輪流量傳感器的信號頻率F，即可在以上檢定結果中檢索各F,值，找出滿足F,≤F≤F的Fi、Fi+1(i=1,2,.，.n-1)，n是該渦輪流量傳感器的流量檢定點數;若信號頻率F=Fi或F=Fi+1，則相應的Ki或K.i+1即為所需的儀表系數;若信號頻率Fi<F<Fi+1，即所測得的信號頻率不正好在檢測頻率點上，此時的儀表系數K可以用線性插值公式(7)來計算:
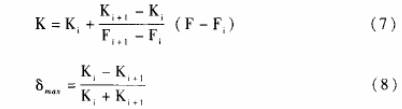
這種計算方法的設計思路是在檢定頻率點上直接用檢定點的檢定儀表系數，其誤差就是該點的重復性誤差δg;在檢定頻率點之間就采用相鄰兩個檢定點的檢定儀表系數K、Ki+1的線性差值得到該點的儀表系數K，由此帶來的最大測量誤差的極限值為K、Ki+1之間的非線性誤差δ?max。因為各計量檢定點是按照鑒定規程(JJG198-94)確定的，所以各檢定點的非線性誤差δ?max與全量程非線性誤差δ之間應滿足δ?max=δ/n.也就是說使用這種計算方法得到的測量結果其誤差值只有采用平均儀表系數時1/n由于渦輪流量傳感器的儀表系數K與流量Q之間當Q≥Q。時基本呈線性關系，所以用線性插值法得到的實際的測量誤差8'更接近重復性誤差ER而遠小于非線性誤差δ?max，即δ'≈En<ER<δ?max。
這種計算方法與平均儀表系數方法的區別在于渦輪流量計的數據存儲區中存放的是n組實際檢定結果而不是一個平均儀表系數`K;使用流量計進行流量測量時，根據測得的頻率值F找到與之相鄰的一對檢定頻率點(Fi,Fi+1)及對應的一對檢定儀表系數(Ki，Ki+1),不是簡單地用測得的頻率值F除以平均儀表系數`K就得到了當前流量值;根據(Fi,Fi+1).(Ki，Ki+1)，先用公式(7)計算出對應信號頻率F的儀表系數K,然后用該頻率值F除以計算得到的儀表系數K得到當前流量Q。這種方法可稱之為“檢定系數折線法"。這種使用方法看似比用平均儀表系數繁瑣，但在目前廣泛采用的微機化儀表中非常容易實現;采用此法在可編程控制器(PLC)以及計算機檢測、控制系統中進行流量測量，可以在確定的量程范圍內提高渦輪流量傳感器的測量精度或者在確保精確測量的前提下擴大測量范圍。
4實驗數據分析
被檢儀表:公稱通徑分別為10mm和15mm的渦輪流量傳感器各一臺;檢定裝置:靜態稱重法標準水流量檢定裝置，系統精度+0.2%。分別采用常規的平均儀表系數法和檢定系數折線法進行標.定，并與作為標準的靜態稱重法的檢定結果進行比對，結果見表1.表2。
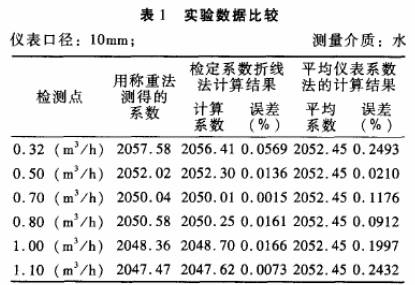
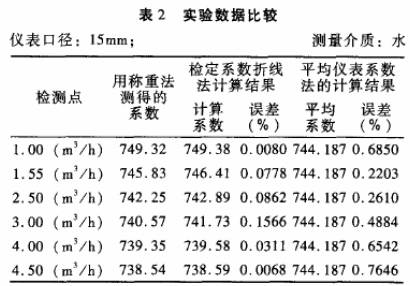
從表1可見，在相同的量程范圍(0.32m3/h~1.10m3/h)內，使用常規平均儀表系數法的最大非線性誤差為0.2493%，而使用檢定系數折線法的最大誤差只有0.0569%，誤差堿少了4倍多;表2顯示，使用常規平均儀表系數法的最大非線性誤差為0.7646%，在相同的量程范圍(0.5m3/h~5.0m'/h)內，檢定系數折線法的最大誤差只有0.1566%，減少了近5倍。顯然，在同樣的測量精度水平(如對10mm渦輪取0.2級、對15mm渦輪取0.5級)下，采用檢定系數修正法渦輪流量傳感器的測量范圍比使用常規的平均儀表系數法有了明顯的擴大。
以上內容源于網絡，如有侵權聯系即刪除!
