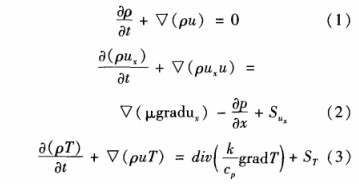摘要:基于渦街理論,分別對(duì)圓形阻流體、正方形阻流體和三角形阻流體所形成的渦街場(chǎng)進(jìn)行仿真研究,同時(shí)對(duì)三種阻流體對(duì)應(yīng)的渦街流量計(jì)進(jìn)行數(shù)值仿真,分析流量計(jì)中應(yīng)變片對(duì)三種阻流體流場(chǎng)壓力和速度的影響.結(jié)果表明,應(yīng)變片改變了流場(chǎng)振蕩的頻率,三角形渦街流量計(jì)的壓力損失最小.
0引言
渦街是在一定條件下的定常流繞過(guò)阻流體時(shí),物體兩側(cè)周期性地脫落出旋轉(zhuǎn)方向相反、排列規(guī)則的雙列線渦.渦流的產(chǎn)生使得阻流體兩側(cè)流體的瞬間速度和壓力不同,因此使阻流體發(fā)生振動(dòng).渦街流量計(jì)通過(guò)嵌人到流體中的漩渦發(fā)生體得到產(chǎn)生的交替漩渦的頻率,通過(guò)頻率與流速成正比的關(guān)系來(lái)測(cè)量流速.
本文基于渦街理論,分別對(duì)圓柱阻流體,正方阻流體和三角形阻流體三者進(jìn)行數(shù)值模擬,并且對(duì)三種阻流體對(duì)應(yīng)的渦街流量計(jì)中的壓電傳感器片對(duì)流場(chǎng)的壓力、速度等參數(shù)的影響進(jìn)行分析.
1數(shù)值模型
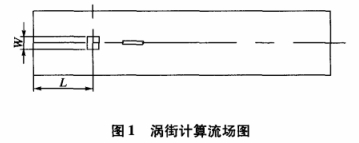
圖1所示方形渦街流量計(jì)的計(jì)算流場(chǎng)圖,流場(chǎng)中繞流體中心距流場(chǎng)入口距離設(shè)為L(zhǎng)=0.2m,.阻流體迎風(fēng)寬度設(shè)為w=0.04m,流場(chǎng)速度設(shè)為0.01m/s.
數(shù)值計(jì)算滿(mǎn)足質(zhì)量、動(dòng)量、能量守恒方程,如方程(1)、(2)和(3)所示.選擇隱式非穩(wěn)態(tài)模型,采用有限體積法中的SIMPLEC(Semi-ImplicitMethodforPressure-LinkedEquationsConsistent)協(xié)調(diào)性壓力耦合方程組的半隱式,計(jì)算采用二階迎風(fēng)格式。
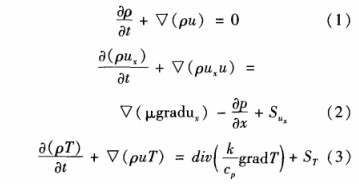
2數(shù)值模型三種阻流體和對(duì)應(yīng)流量計(jì)算結(jié)果及分析
本文針對(duì)圓形、正方形和三角形三種阻流體分別進(jìn)行壓力和速度的分析,并對(duì)流場(chǎng)中中心線上的壓力和速度變化進(jìn)行具體闡述.
2.1三種阻流體壓力流場(chǎng)分析
圖2為三種阻流體渦街場(chǎng)和渦街流量計(jì)流場(chǎng)總壓力分布云圖.由圖所示,圓形阻流體后部流場(chǎng)中漩渦交替分布比較有規(guī)律,渦街現(xiàn)象明顯.對(duì)于正方形阻流體,距離阻流體較近時(shí),仍能看到比較明顯的漩渦分布,而后漩渦逐漸散開(kāi).對(duì)于三角形阻流體,低壓漩渦形狀比較圓整,漩渦分布比正方形阻流體規(guī)則.另外,不同形狀阻流體的分離點(diǎn)不同,圓柱沒(méi)有其固定分離點(diǎn),整個(gè)半圓面都可以;正方形的分離點(diǎn)則會(huì)出現(xiàn)在前方尖點(diǎn)及附近邊或者后方尖點(diǎn)及附近邊;三角形則有其固定分離點(diǎn),主要集中在前方兩個(gè)尖點(diǎn)及其附近的邊上.對(duì)于渦街流量計(jì)流場(chǎng),由于應(yīng)變片在阻流體后的加入,改變了流場(chǎng)中擾動(dòng)的頻率,三種不同流量計(jì)的流場(chǎng)中頻率均變低,這是因?yàn)橐后w在遇到金屬應(yīng)變片之前還未形成規(guī)則的漩渦,在金屬應(yīng)變片邊緣發(fā)生剝離,由于三種阻流體的剝離點(diǎn)影響,低壓場(chǎng)的范圍三角形最大,正方形次之,圓形最小。
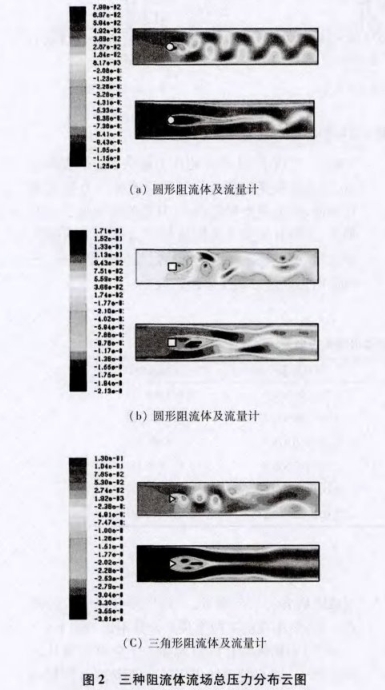
由圖可以看出,阻流體前端的壓力保持恒定,而后在阻流體和應(yīng)變片之間流場(chǎng),壓力急劇下降,形成局部低壓區(qū).正方形渦街流量計(jì)壓力變化應(yīng)變片的后端波動(dòng)較大,圓形渦街流量計(jì)次之,三角形渦街流量計(jì)應(yīng)變片后的壓力變化比較平穩(wěn)。
2.2三種阻流體流場(chǎng)中心線速度分析
圖3為三種阻流體渦街流場(chǎng)中心線速度分布,以流場(chǎng)左側(cè)人口為位置初始點(diǎn),橫坐標(biāo)為中心線上各點(diǎn)到初始點(diǎn)的距離,縱坐標(biāo)為速度大小.由圖可以看出,初始流速大小相同,當(dāng)遇到阻流體時(shí),流速急速下降,在阻流體中心點(diǎn)0.2m前后對(duì)應(yīng)的兩個(gè)位置處速度降為0,形成速度駐點(diǎn).比較不同阻流體,對(duì)于圓形阻流體,阻流體后的流速發(fā)生周期振蕩并有上揚(yáng)趨勢(shì);對(duì)于正方形阻流體,阻流體后的流速發(fā)生一定振蕩;對(duì)于三角形阻流體,阻流體后的流速振蕩比較明顯.這表明阻流體在流場(chǎng)中引起的擾動(dòng)比較大,使得阻流體后的速度發(fā)生不規(guī)則振蕩.
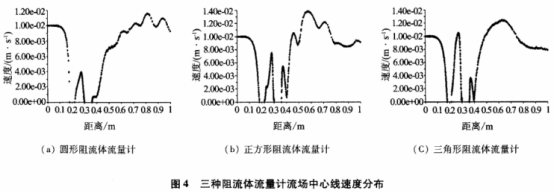
圖4為三種阻流體渦街流量計(jì)流場(chǎng)中心線速度分布.在渦街流量計(jì)流場(chǎng)中,流速在阻流體前急劇下降,阻流體前后對(duì)應(yīng)的兩個(gè)位置處為速度駐點(diǎn),并在應(yīng)變片前部形成了新的速度駐點(diǎn).與圖3相比,阻流體前流速變化相同,由于應(yīng)變片的嵌人,后部的流速震蕩頻率變低,并且渦街流量計(jì)流場(chǎng)的最大速度和平均速度要比對(duì)應(yīng)的阻流體渦街場(chǎng)小對(duì)于圓形阻流體流量計(jì)流場(chǎng),應(yīng)變片后部的速度振蕩頻率約為渦街流場(chǎng)的一-半.對(duì)于正方形阻流體,應(yīng)變片后最高速度的位置從0.83m提前至0.7m處.對(duì)于三角形阻流體,應(yīng)變片后的流速明顯變得平滑,尤其是從0.4m開(kāi)始,振蕩周期變大,同時(shí)速度在0.65m處為最大值,隨后逐漸下降.
2.3三種阻流體壓力損失
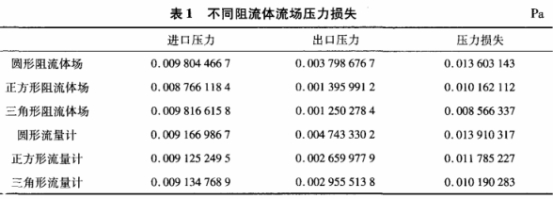
表1所示為不同阻流體壓力損失計(jì)算值,由表可以看出,相同條件下,不同形狀的阻流體的流場(chǎng)中,對(duì)應(yīng)的壓力損失是不同的.圓形阻流體所產(chǎn)生的壓力損失最大,正方形次之,三角形阻流體的渦街場(chǎng)壓力損失最小.比較不同形狀阻流體流量計(jì)可以看到,圓形阻流體流量計(jì)流場(chǎng)的壓力損失最大,三角形阻流體的壓力損失最小.結(jié)果顯示,壓力損失變化趨勢(shì)與三種阻流體壓力損失變化相同,壓力應(yīng)變片的嵌人,只是略微增加了壓力損失,并沒(méi)有改變?nèi)N阻流體壓力損失之間的大小對(duì)比關(guān)系.在三種不同形狀阻流體流量計(jì)中,三角形渦街流量計(jì)的壓力損失最小。
3結(jié)論
(1)在相同條件下,圓形繞流體仿真場(chǎng)可以得到規(guī)律的渦街現(xiàn)象.不同形狀阻流體的分離點(diǎn)不同,圓柱沒(méi)有其固定分離點(diǎn),整個(gè)半圓面都可以;正方形的分離點(diǎn)則會(huì)出現(xiàn)在前方尖點(diǎn)及附近或者后方尖點(diǎn)及附近;三角形則有其固定分離點(diǎn),主要集中在前方兩個(gè)尖點(diǎn)及其附近的邊上;
(2)渦街流量計(jì)的阻流體和傳感器應(yīng)變片之間會(huì)形成一片低速低壓局部場(chǎng),渦街流量計(jì)流場(chǎng)的最大速度和平均速度要比對(duì)應(yīng)的阻流體渦街場(chǎng)小;
(3)三種不同渦街流量計(jì)的振蕩頻率要低于對(duì)應(yīng)的渦街場(chǎng),比較不同形狀阻流體渦街流量計(jì),三角形渦街流量計(jì)的壓力損失為最小.
本文來(lái)源于網(wǎng)絡(luò),如有侵權(quán)聯(lián)系即刪除!