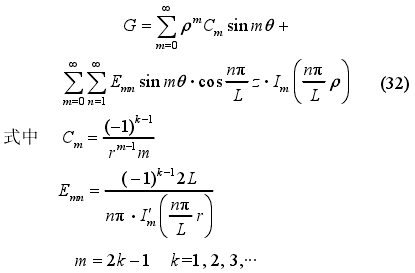摘要:現有電磁流量計干標定模型中,電極尺寸、位置均被作了理想化處理,即假設電極尺寸無窮小、電極位于測量管段正中間的兩個對稱點上,兩對稱點連線與磁場垂直。這類理想化的模型與實際情況差異較大,限制了干標定的精度,并對產品-致性提出了要求。針對這一一問題,采用分離變量法建立了包含實際流量計電極尺寸及位置參數的電磁流量計干標定模型,比現有干標定模型更接近于實際流量計,有利于提高干標定精度,降低對產品一致性的要求。通過與現有模型及數值仿真的對比分析,驗證了該模型的正確率。
0前言
電磁流量計作為一種液體流量計量儀表,計量精度已達到±0.5%以上,口徑范圍由3mm到4000],其中直徑1m以上的大口徑電磁流量計產品在水利工程、市政建設和環境保護等領域中具有非常廣泛的應用。目前,電磁流量計的標定方法包括實流標定及干標定兩種。實流標定的精度一般為±0.2%以上,被絕大多數電磁流量計廠家采用。但實流標定存在兩個缺陷:①大口徑流量計實流標定裝置制造價格昂貴,標定成本高。如:實流標定1.2m口徑的儀表,需要250kW的水泵連續提供約1.5t/s的流量,標定時間約2~4h,標定裝.置造價約300萬英鎊;②實流標定裝置所產生的流場通常為理想流場,很難利用現有的實流標定裝置對多相流、漿液、粘性介質等非常規介質進行標定,在這類實流標定裝置上進行模擬各種現場工況的流體運動學和動力學特性研究也十分困難。相比之下,電磁流量計干標定技術作為一種無需實際流體便可實現流量計標定的技術,在降低標定成本、裝置制造成本,以及模擬各種實際流場、介質等方面,具有獨特優勢。
電磁流量計干標定方法的核心是數學模型,數學模型的完善與否決定了干標定的精度、對產品一致性要求等特性。最完善的干標定模型應包含實際流量計的所有有用信息,以便更好地體現每臺流量計的個體差異,使模型更加接近于實際流量計。現有干標定模型主要采用物理學家為分析、改進電磁流量計性能所建立的理想數學模型稱之為理想數學模型是因為在某些參數上,模型不考慮實際流量計的數值及個體差異,進行了理想化處理。這些模型在相應的理想情況下具有足夠的精度,理想化處理又降低了模型推導的數學難度,因此,在分析、改進電磁流量計性能方面被認為是非常成功的。但就干標定模型應盡可能地包含實際流量計所有有用信息的要求而言,這些理想模型用于千標定尚不夠完善,被理想化處理的參數成為了干標定模型的誤差源,導致了現有干標定技術與實流標定技術相比精度較低(普遍低于±0.5%,與標定0.5級電磁流量計所需的±0.2%仍有-定差距)、對產品一致性的要求較高,限制了干標定技術更好的工業化應用。因此,建立更接近實際.流量計,即包含更多實際流量計信息的干標定模型,是改進電磁流量計干標定技術的重要任務。
電極尺寸與位置便是現有電磁流量計干標定模型中被理想化處理的因素之--,現有模型中往往存在如下理想化處理:兩電極的面積都為零,即理想的數學點;電極所在位置為測量管段正中間的兩個對稱點,其連線與磁場嚴格垂直。但實際流量計中,電極并非理想的數學點,也無法正確地安裝在管段正中間的兩個對稱點上,這使其成為了電磁流量計干標定模型與實際流量計的差異之一。
針對此問題,本文采用分離變量法建立了包含實際流量計電極尺寸及位置參數的電磁流量計干標定模型,比現有干標定模型更接近于實際流量計,有利于提高干標定精度、降低對產品一致性的要求,并進一步驗證了模型的正確率。
電磁流量計干標定方法
1.1電磁流量計測量原理
電磁流量計測量原理如圖1所示,管道內流動的導電液體切割磁力線,將在兩端電極A、B間產生電勢差UAB,UAB與磁通量密度B、液體流速v符合弗來明右手定則,從而通過測量UAB的大小可確定管道內介質流量。
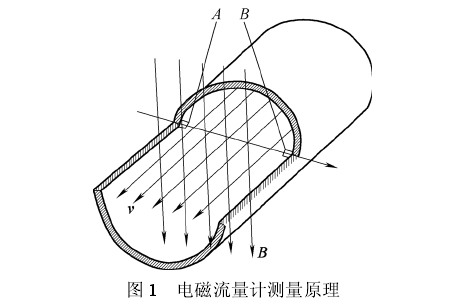
當不考慮位移電流時,可從麥克斯韋爾方程組推導出電磁流量計的基本微分方程如下。
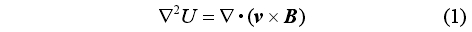
式中,U是感應電動勢,v為被測流體速度,B為.測量空間內磁通密度,V2為拉普拉斯算子,▽為哈密爾頓算子。
1.2干標定基本數學模型
電磁流量計干標定模型需是可計算的數學表達式,因此需將微分方程式(1)轉變成積分式。
由于測量管道內壁除電極外都為絕緣體,即邊界上沒有法向電流(jn=0),且測量兩個電極的電位差時,電極處不能有電流,因此,有邊界條件

式中
τ一電磁流量計測量空間
W一權重函數,W=▽G
式(5)便是用于電磁流量計干標定的基本數學模型,其中權重函數W的物理含義為:電磁流量計有效測量空間內任意微小流體微元切割磁力線所產生的感
應電勢對兩電極間的電勢差所起的作用大小。可見,若能分別得知vB、W隨空間坐標的表達式及測量空間τ,可通過式(5)計算出電極間輸出電勢差UAB,這便是電磁流量計干標定的基本原理。
v隨空間坐標的表達式可通過流場分析得到,也可通過不同表達式實現不同流場、介質的模擬,B隨空間坐標的表達式則可通過特殊的磁場測量方法得到,測量空間τ可通過測量管段的結構尺寸得知,而W隨空間坐標的表達式,則需通過W=▽G計算得到。G滿足拉普拉斯方程式(3),其邊界條件式(4)包含的信息為:管段尺寸、電極尺寸及電極位置。因此,電極尺寸、電極位置為求解權重函數W的數學表達式所必需的信息。若簡單地將電極尺寸及位置做理想化處理,而忽略實際流量計中電極存在尺寸往往無法被準確地安裝到管段正中間兩個對稱點上的事實,將不利于獲取高精度的電磁流量計干標定模型。
2包含實際電極尺寸及位置參數的干標定模型
上述分析說明,有必要在建模過程中考慮實際流量計的電極尺寸及位置。因此,將半徑為r、長度為2L的電磁流量計一次傳感器按如下方式建模:ρ、θ向尺寸及位置如圖2a所示,電極A所覆蓋范圍為(ρ=r,γA-△ϒA≤θ≤γA+△γA),電極B所覆蓋范圍為(ρ=r,γB-△γB≤θ≤γB+△γB),其中γA、△γB為表示電極θ向位置的變量,△γA、△γB為表示電極θ向尺寸的變量,若按照理想點電極處理,則△γ=π/2,γB=-π/2,△γA=△γB=0;z向尺寸及位置如圖2b所示,電極A所覆蓋范圍為(ZA-△ZA≤Z≤ZA+△ZA),電極B所覆蓋范圍為(ZB-△ZB≤z≤ZB+△ZB),其中ZA、ZB為表示電極z向位置的變量,△zA小、△zB為表示電極z向尺寸的變量,若按照理想點電極處理,則zA=zB=0,△ZA=△ZB=0。
從以上分析可知,要得到干標定模型,便需得到權重函數W的數學表達式,即先在柱坐標系(ρ,θ,z)下求解式(3)。
求解式(3)的邊界條件式(4)可化為

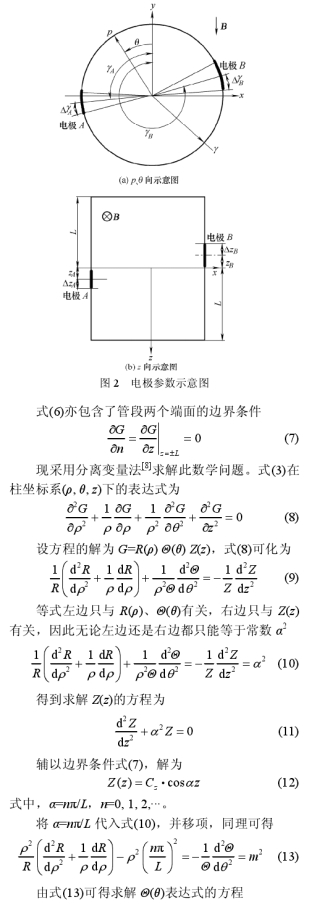


3模型正確率的驗證
干標定模型中,新建立的模型與以往模型相比,差別只在于權重函數w表達式的不同,因此只需對權重函數W或W的上級函數Green函數G的表達式進行驗證,便可完成對干標定模型正確率的驗證。最理想的模型驗證方式是直接測量出電磁流量計測量空間內各點的權重函數值,與模型計算所得值計進行比較,但目前尚未有成熟的權重函數測量方法。若直接將模型運用到干標定系統中,與實流標定進行試驗對比,則由于電磁流量計干標定模型中還包括磁場信息,會將磁場測量與計算誤差引入其中,導致無法對模型的正確率做出客觀的評價。因此,采用以下驗證方式:將現有典型理想模型的電極參數代入所建立的干標定模型,與相應的理想模型進行比較,驗證所建干標定模型在理想參數下的正確率;利用數值仿真,計算考慮實際電極尺寸與位置時測量空間內若干點的權重函數數值,與干標定模型計算所得數值進行對比。
3.1與理想模型比較
選用SHERCLIFF國的線形電極模型及文獻[1]中的點電極模型進行比較,如上所述,只需就權重函數W或W的上級函數Green函數G的表達式進行比較即可。
SHERCLIFF所建立的線形電極模型基于理想的線形電極電磁流量計,且假設磁場B的方向與y軸平行,即Bx=Bs=0,流速v的方向與:軸平行,即vx=vy=0。
將以上式子代入本文所建立的干標定模型,可得

此結果與SHERCLIFF所得到的W表達式一致,即在線形電極情況下,模型一致。
建立的點電極模型基于理想的點電極流量計,電極尺寸及位置參數如下:△γA→0、△γB→0、△ZA→0、△ZB→0、γA=π/2、γB=-π/2、ZA=0、ZB=0。
將以上參數代入式(18),Dm及Fmn有關項都將為零,代入Cm表達式(21)及Emn的表達式(24),并進一步化簡后,可得Green函數G的表達式為
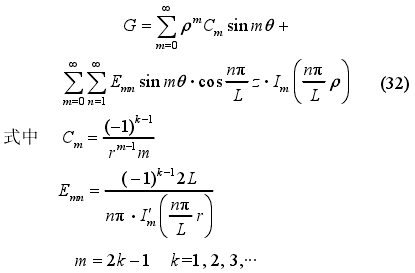
此結果與文獻凹得到的Green函數表達式相同,即在點電極情況下,模型--致。需說明的是,王竹溪的模型中正x軸對應θ=0,而非圖2所示的正y軸對應θ=0,式(32)已是將所建立的模型坐標調整至與模型坐標相同后的結果。
3.2與數值計算比較
在電磁流量計電極兩端加上電壓信號,測量空間內所形成的電場與權重函數具有相同的分布特性,因此可采用電場數值仿真的方式對權重函數模型進行驗證。通過理想模型、包含實際電極參數的模型及數值仿真三者計算結果的比較,可較為明顯地看出考慮實際電極尺寸與位置參數與否的差別。
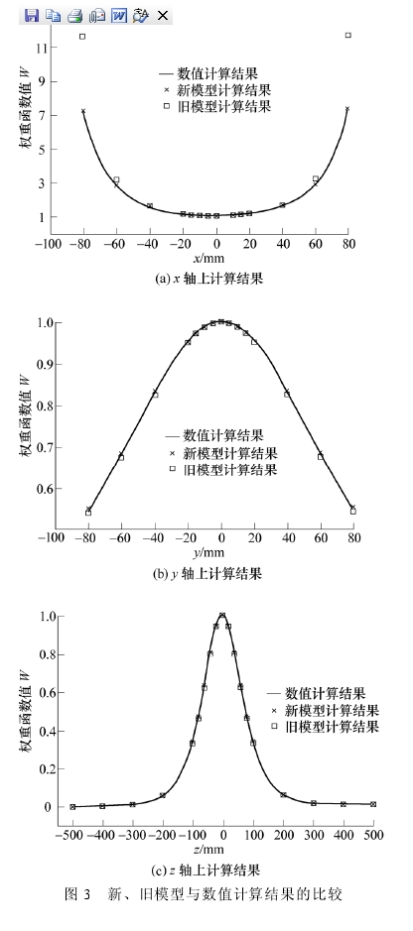
所比較流量計的參數為:r=100mm、L=500mm、△ϒA=△ϒB=5°、△ZA=△ZB=rx5°、ϒA=95°、ϒB=-85°、ZA=rx5°、ZB=--rx5°,且假設磁場B的方向與y軸.平行,即B,=B:=0,流速v的方向與=軸平行,即vx=vy=0,則可由W的x分量Wx代替W。利用理想點電極模型、新建立的干標定模型及按實際電極參數所建立的數值仿真模型,分別對x、y與=軸上的權重函數數值進行計算。結果如圖3所示,圖中新、舊模型分別指新建立的包含電極尺寸與位置信息的干標定模型、理想點電極模型,對其中圖3a所示的x軸上計算結果進行分析,可清晰地發現新模型較舊模型與數值計算結果更吻合,忽略實際電極尺寸與位置參數將帶來較大的誤差,尤其是在靠近電極的位置。計算結果還顯示,在所給出的參數下,y與:軸上的權重函數受參數影響較小,但隨著電極尺寸的加大及電極位置越來越偏離理想位置,y與:軸上的數值將呈現與x軸類似的現象,即舊模型的計算誤差越來越大,新模型則能很好地與數值計算吻合。
4結論
指出現有電磁流量計干標定模型過于理想化,并不能完全滿足干標定的技術要求,要解決干標定.技術精度較低、對產品一致性要求較高的缺點,有必要建立更接近實際流量計,即包含更多實際流量.計信息的干標定模型。就現有模型中將電極尺寸、位置作理想化處理,即假設:電極尺寸無窮小、電極位于測量管段正中間的兩個對稱點上且其連線與磁場垂直,致使模型與實際流量計存在差異的缺點,采用分離變量法建立了包含實際流量計電極尺寸及位置參數的電磁流量計干標定模型,模型比現有模型更接近于實際流量計。對新建立的干標定模型作了如下驗證:①選用線形電極模型、點電極模型為比較對象,將這兩種典型理想模型的電極參數代入所新建立的干標定模型進行計算,結果與這兩種典型理想模型一致;②分別采用理想點電極模型、新建立的干標定模型及數值仿真,對參數為r=100mm、L=500mm、△ϒa=△ϒB=5°、△zA=△zB=ϒx5°、ϒA=95°、ϒB=-85°、ZA=ϒx5°、zB=ϒx5°的流量計權重函數數值進行了計算,結果顯示新建立的干標定模型與數值計算結果吻合,而忽略實際電極參數的理想點電極模型則存在較大的計算誤差。通過以上驗證,證明了所建立模型的正確率,亦說明了建立此類更完善的電磁流量計干標定模型的必要性。
本文來源于網絡,如有侵權聯系即刪除!