1 引 言
1. 1 轉(浮)子流量計的特點及其應用
轉(浮)子流量計是常用的氣體流量測量設備,具有結構簡單、使用維護方便、對儀表前后直管段長度要求不高、壓力損失小且恒定、測量范圍比較寬、工作可靠、適用性廣等特點,但是其流量特性易受流體粘度、密度等影響。就是說,同一只轉(浮)子流量計,用于不同介質條件下的同一體積流量測量時,可能得到不同的測量結果,由此便造成測量誤差。
氣體轉(浮)子流量計出廠時的刻度一般是用空氣標定給出的[1]。因此,當用其測量其他氣體介質流量時,必須對儀表刻度進行合理修正。對此,文中給出了介質粘度相近而密度不同時的流量修正公式,作為進行不同介質間流量換算方法的參考。公式并不復雜,但是真要做到深入地理解公式的背景以及靈活掌握其應用場合,卻并不簡單。
1. 2 問題的提出
航天型號工程上經常使用氦氣這種自然界中密度最小的惰性氣體。在評價某些部件的性能指標時,需要使用轉(浮)子流量計測量氦氣流量。
在轉(浮)子流量計氦氣流量的校準問題上,一些觀點主張用空氣檢定,然后按文獻[ 2]的方法將空氣流量值換算成氦氣的流量值。然而,當我們分別用空氣和氦氣兩種介質對轉(浮)子流量計進行檢定/校準后發現,按該方法對空氣流量刻度修正后得到的氦氣理論計算結果與實際氦氣流量相差很大。
為了說明該問題,我們選擇型號為LZB -10的氣體轉子流量計,先用空氣檢定,其空氣刻度流量示值合格,然后再用氦氣介質對其五個刻度點進行氦氣流量校準,將同一刻度下所得氦氣流量實測值和空氣流量刻度值、單純密度修正后的氦氣流量計算值以及文獻[ 2]修正方法中的理論密度修正系數和實際綜合修正系數進行比較后,得到表1中的數據。
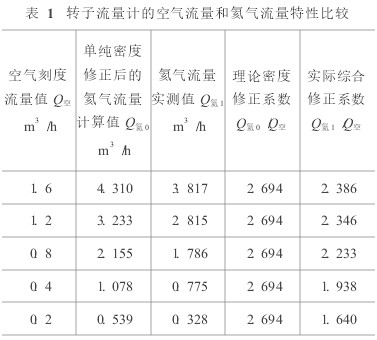
從表1可看出:
a)實際氦氣流量與空氣流量并不遵循文獻[ 2]所述的單純密度修正關系(即:實際綜合修正系數并不等于理論密度修正系數);
b)實際綜合修正系數小于理論密度修正系數,即:實際氦氣流量小于單純密度修正后得到的理論氦氣流量;
c)理論密度修正系數是常數,與流量無關,而實際綜合修正系數與流量有關,并隨著流量的減小而減小。
為什么會出現上述現象理論數據與實驗結果間的不一致性究竟說明了什么問題能否在理論上解釋得通所有這些就是本文重點要探討的問題。其實,這也是對氣體轉(浮)子流量計流量特性的介質相關性原理及其流量修正方法適用性問題的深入理解和重新認識。這一點非常重要,因為只有這樣,才能真正做到理論與實踐的統一,確保量值傳遞的正確性。
想要弄清楚提出的上述問題,需首先從轉(浮)子流量計的結構及工作原理說起。
2 轉(浮)子流量計的結構及工作原理簡述[ 3,4]
轉(浮)子流量計主要由錐管、浮子和支撐連接結構組成。流量標尺直接刻在錐管上,標示了浮子高度與被測介質流量間的一一對應關系。圖1為其工作原理示意圖。
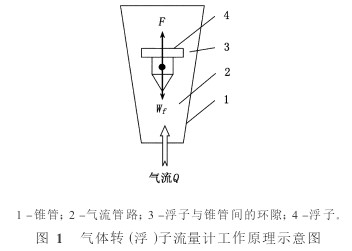
在一垂直錐形管中放有浮子,當流體自下而上流過時,依據伯努利方程,浮子前后會形成差壓,此差壓形成一個使浮子上升的力F。當F大于浸在流體內浮子的重力Wf時,浮子上升。隨著浮子的上升,浮子最大外徑與錐形管之間的環形面積逐漸增大。在流量保持不變的情況下,流速逐漸減小,于是F也逐漸減小,直到F和Wf相等時,浮子就穩定在某一高度。同時,考慮到實際流動情況和理想狀態間的差異,可得到F和流體密度ρ、流速v、浮子最大橫截面積a間的關系為
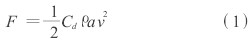
式中:Cd———阻力系數,由校準實驗獲得,與浮子形狀、流體流動狀態、流體的物理性能有關。
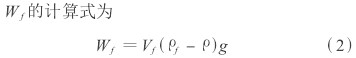
式中:Vf———浮子體積,m3;ρf———浮子材料密度,kg /m3;g———重力加速度,m /s2。
由式(1)與式(2)相等的關系,我們可以得到流量Q的計算公式為
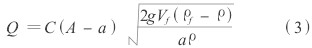
式中:C———流量系數;A———錐管管路截面積,m3。
對于氣體介質來說,ρ遠小于ρf,于是上式便簡化為式(4),此即氣體轉(浮)子流量計的流量測量原理。
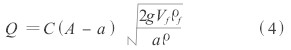
3 轉(浮)子流量計流量特性的介質相關性修正
對于某一特定流量計,式(4)中的A,a,Vf、ρf等與流量計結構或浮子材料有關的參數便已確定,同時注意到,公式中還有流量系數C、密度ρ兩個參數與被測流體有關。只要選定了流體介質,通過刻度標定或流量校準實驗便可為該流量計定標或確定浮子高度與實際流量間的對應關系。因此,某一特定轉(浮)子流量計出廠時錐形管上均標明了現有刻度適用的介質種類,當其用于不同于刻度適用介質的其他介質流量測量時,須對刻度進行合理修正。由以上分析知,轉(浮)子流量計流量特性的介質相關性修正應包括密度的修正和流量系數的修正,而流量系數又與流體粘度有關,因此流量系數修正有時也稱粘度修正。
3. 1 密度修正
密度的修正就是文獻[2]中提到的修正方法,比較簡單:設刻度介質的流量為Q0、密度為ρ0,被測流體的流量為Q1、密度為ρ1,則依據式(4),可得到流量對密度的修正公式為
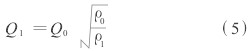
由此可見,流量與密度的平方根成反比,此即轉(浮)子流量計的密度修正原則。
3. 2 流量系數修正
對于流量系數C的修正,則比較復雜。在理想情況下(假設流體為理想流體,完全沒有粘性;假設流動為理想流動,完全沒有能量損失),C是恒等于1的常數。然而,實際應用中不可能出現上述絕對理想的狀態。
實,對于某一特定流量計,流量系數可表示為雷諾數Re的函數[4],而雷諾數表征流體流動時慣性力與粘性力之比的無量綱數[5],由式(6)定義

式中: υ———流動截面的平均流速,m /s;L———流體的特征長度,m;ν———流體的運動粘度,m2 /s。
雷諾數是流量計量中一個重要的參數。當外部幾何條件相似,雷諾數相同時,流體流動狀態也幾何相似,這就是流體力學的相似原理。
可見,流體粘度對流量系數(或流量)的影響在雷諾數中得到了體現。
在流體力學中,流體的粘度有兩個不同的表述術語,很容易使人混淆,一個是動力粘度μ,另一個就是式(6)中的運動粘度ν,二者與流體的密度ρ間的關系見式(7)。

根據雷諾數的定義可知,流體運動粘度ν越大,雷諾數Re就越小,表明粘性力對流體流動的影響較慣性力對流體運動的影響越顯著,流體介質粘性對流量的影響就越不能忽略;反之,流體運動粘度ν越小,雷諾數Re就越大,表明粘性力對流體流動的影響較慣性力對流體運動的影響越不顯著。由此可得出結論:流體粘性對流量的影響程度應以運動粘度ν作為判據,而不應以動力粘度μ作為判據。這一點很重要,它對于氣體轉子流量計的計量檢定工作具有指導意義,如果以動力粘度作為判據,則可能會得出不符合實際的結果,因為動力粘度相近的氣體,其運動粘度則可能相去甚遠。以空氣和氦氣為例,在標準狀態下,空氣和氦氣的動力粘度分別為[6]:1. 81×10-5Pa? s,1. 97× 10-5Pa? s,應該說很接近,但由于二者的密度相差很大,分別為:1. 205 kg /m3,0. 1663 kg /m3,導致二者的運動粘度也相差很大,分別為:1. 502× 10-5m2 /s和11. 85× 10-5m2 /s。
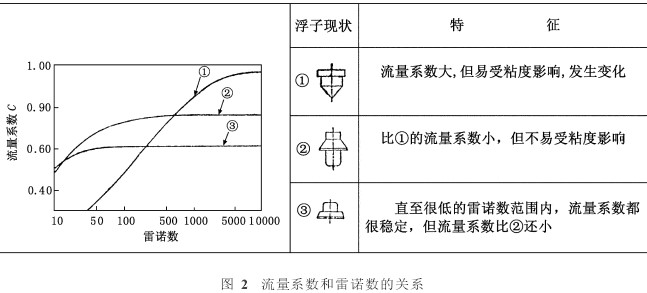
對于不同的流量計,由于結構本身及浮子形狀的不同,流量系數C與雷諾數Re的關系也不盡相同,我們很難找到一個通用的理論公式進行表述,一般通過大量實驗數據以曲線的形式描繪二者的特定關系。在這方面,日本學者也進行了比較深入地研究,其中,文獻[4]也給出了不同浮子形狀的流量計,其流量系數C與雷諾數Re的關系曲線,見圖2。
從圖中看出,對于具有確定浮子形狀的轉(浮)子流量計,如果氣體介質的運動粘度足夠的小,致使雷諾數Re大到一定數值后,其流量系數C便基本保持不變。因此,在該區域(暫且稱之為線性區域),不需要進行粘度修正(或稱流量系數修正),只需進行密度修正就可以了。可是,對于氦氣來講,由于其運動粘度相對空氣大很多,導致其雷諾數與空氣的雷諾數也相差很大,于是出廠時只用空氣標定過的流量計,在用于氦氣流量測量時,不一定工作在線性區域內,二者的流量系數可能會發生差異,而且測氦氣流量時的流量系數較空氣時小。很顯然,這就解釋了本文引言中引出的a和b兩個現象:對氦氣流量進行單純密度修正是不科學的,即綜合修正系數實際包含了密度修正和流量系數修正;氦氣實際流量比只做密度修正得到的理論換算流量小。
此外,結構形狀已確定的浮子的邊緣厚度在不同介質運動粘度條件下對流量系數的影響[4],見圖3。
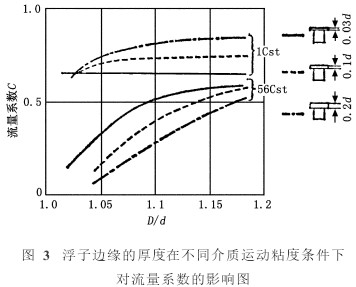
圖中,橫坐標為流量計錐管直徑D和浮子直徑d之比,即表示浮子的高度位置或流量刻度。圖中按運動粘度的不同給出了兩組流量系數曲線,上面一組為1Cst(Cst為運動粘度單位,1Cst= 10-6m2 /s)時的曲線,下面一組為56Cst時的曲線。從圖中可看出兩個現象:
●在浮子形狀結構確定了的情況下,流量系數與流體運動粘度有關,運動粘度越大,則流量系數越小;
●一般情況下,同一流量計的不同流量刻度位置,流量系數也可能不同。流量越小,系數也越小。不過,對于較小運動粘度的流體,流量系數與流量刻度位置的相關性越小;流量系數與刻度位置的相關程度,還取決于浮子形狀。
該圖還進一步旁證了以下兩個現象:
●流體粘性對流量的影響程度應以運動粘度ν作為判據,而不應以動力粘度μ作為判據;
●對于氦氣流量來說,對空氣流量刻度的實際綜合修正系數與流量有關,并隨著流量的減小而減小。此即對本文引言中引出的c)現象的解釋。
4 結論
總結前面的理論分析和實驗數據,結合實際工作經驗,對于氣體轉(浮)子流量計的介質相關性問題,我們有以下幾點理解與讀者分享,而這幾點卻往往是轉子流量計校準工作中容易被忽視的地方:
●轉(浮)子流量計流量特性的介質相關性體現在兩個方面:密度相關和運動粘度相關。分別對應不同氣體介質流量間的密度修正(換算)和流量系數修正(換算),只是在滿足一定條件的前提下,可只進行密度修正(換算);
●應正確理解文獻[ 2]的密度修正方法中提到的粘度相近原則。由于流體粘度有動力粘度和運動粘度之分,因而在此相近原則的理解上容易產生歧義。事實上,同一只流量計,用于測量不同氣體介質流量時,其流量系數的不同源于介質運動粘度的差異,而不是動力粘度的差異。因此,應以二者運動粘度的相近程度來作為是否只進行密度修正的判據,而不應以動力粘度作為判據,否則,便有失科學性。比如:動力粘度相近而運動粘度相遠的氦氣和空氣流量間的關系就是一個活生生的例子。
對于與空氣運動粘度差別很大的氣體介質(如:氦氣),當然不能只進行密度修正。但是由于流量計整體結構及浮子形狀的千差萬別,流量系數(或粘度)的修正,很難像密度修正那樣找到一個合適的理論公式。在此情形下,用實際工作介質對流量計刻度的重新校準是一種科學的選擇,因為這樣就可以直接得到工作介質的真實流量,而不必再進行理論換算。
5 結束語
轉(浮)子流量計結構雖然很簡單,其在流量測量中的應用也很常見,然而,由于流量計量特性的介質屬性相關性以及流體物理性質的千差萬別,注定了流量計量技術的復雜性,尤其是氣體介質比較顯著的可壓縮性及熱膨脹性,則更加大了氣體流量校準難度。
以上只是我們實際工作中獲得的一些粗淺經驗和思考,有關轉(浮)子流量計氦氣流量特性的更加深入地探索工作,有待眾多的流量計量科研工作者的共同努力。
以上內容來源于網絡,如有侵權請聯系即刪除!